Crowdly
Add to Chrome
20300 - Matemàtica Discreta. Grup 01,02, 03, 10 i 11
Looking for 20300 - Matemàtica Discreta. Grup 01,02, 03, 10 i 11 test answers and solutions? Browse our comprehensive collection of verified answers for 20300 - Matemàtica Discreta. Grup 01,02, 03, 10 i 11 at ad.uib.es.
Get instant access to accurate answers and detailed explanations for your course questions. Our community-driven platform helps students succeed!
Donau el residu de la divisió entera de -2022 entre 20.
View this question
Resoleu l'equació 1092x≡243 (mod 2295). Si té solució, donau la solució x més petita estrictament positiva (sense els [ ] al voltant). Si no té solució, responeu NO (en majúscules).
View this question
Considera l'aplicació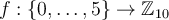 
f:\{0,\ldots,5\}\to \mathbb{Z}_{10} definida per ![f(n)=[3n]](https://firebasestorage.googleapis.com/v0/b/crowdvns.appspot.com/o/files_v4%2Fad_uib_es%2Fquestions%2Fe33fc99abb6dee902eb50c47acfb73148c3bcdb30ad28b1abc185fd602d85b18%2Fresources%2F4e00b61fc54fdaef313cbbace097e06ad673cf7c44e98b1bbca4389b15e8b0b1?alt=media)
f(n)=[3n]. Quina de les afirmacions següents és correcta? Marca una sola resposta.
❌
❌
❌
❌
✅
View this question
Dóna el coeficient de 33 en la identitat de Bézout que produeix l'algorisme d'Euclides aplicat a 39 i 33.
View this question
Resoleu l'equació 1092x≡214 (mod 2295). Si té solució, donau la solució x més petita estrictament positiva (sense els [ ] al voltant). Si no té solució, responeu NO (en majúscules).
View this question
Considerau l'aplicació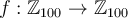 
f:\mathbb{Z}_{100}\to \mathbb{Z}_{100} definida per ![f([x])= [21x]](https://firebasestorage.googleapis.com/v0/b/crowdvns.appspot.com/o/files_v4%2Fad_uib_es%2Fquestions%2F15fd7cf104daada8e234c995f9fa788e34e640664df74e115eca9063ae9418fd%2Fresources%2Fe41da9c210fae57e691c94a4d1f56d41a41475440e02977c95050c4c6d880c2a?alt=media)
f([x])= [21x]. És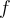 
f bijectiva? I en cas afirmatiu, qui és ![f^{-1}([2])](https://firebasestorage.googleapis.com/v0/b/crowdvns.appspot.com/o/files_v4%2Fad_uib_es%2Fquestions%2F15fd7cf104daada8e234c995f9fa788e34e640664df74e115eca9063ae9418fd%2Fresources%2F277f4e1ccd49abdb13b379de1f515d16150b70c26bdf98babb8c54ffca0d966c?alt=media)
f^{-1}([2])? Si 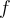f és bijectiva, la resposta ha de ser SI (en majúscules, sense accent) seguit d'una coma i de la antiimatge demanada (exemple de resposta en format correcte: SI,[0]); si 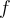f no és bijectiva, la resposta ha de ser NO (en majúscules) i res més.
View this question
Sobre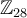 
\mathbb{Z}_{28} considerau la relació d'equivalència ![[x]\sim [y]](https://firebasestorage.googleapis.com/v0/b/crowdvns.appspot.com/o/files_v4%2Fad_uib_es%2Fquestions%2Fb7c68e0dcbdbd60b3b274b470274d447ece14b3e795db1f835b0ad32cbe102ca%2Fresources%2F4dd9779869d8e067b29d44a58d5a7f407a7ecd8d8a5423e8eda6b8b8514668c5?alt=media)
[x]\sim [y] si, i només si, ![[4][x]=[4][y]](https://firebasestorage.googleapis.com/v0/b/crowdvns.appspot.com/o/files_v4%2Fad_uib_es%2Fquestions%2Fb7c68e0dcbdbd60b3b274b470274d447ece14b3e795db1f835b0ad32cbe102ca%2Fresources%2Fa2180db406c4d79dd4d4735037eb9299d4c2ee509212c401ba0462ff07bf4d69?alt=media)
[4][x]=[4][y]. Quants elements té la classe d'equivalència de l'element [2]? El resultat ha de ser un nombre natural i res més.
View this question
Donau la solució x positiva més petita del sistema d'equacions x≡3 (mod 236), x≡55 (mod 376).
View this question
És veritat que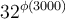 
32^{\phi(3000)} és congruent amb 1 mòdul 3000?
✅
❌
View this question
La relació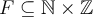 
F\subseteq \mathbb{N}\times\mathbb{Z} definida per 
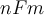nFm si, i només si 
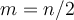m=n/2 si 
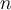n és parell o 
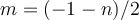m=(-1-n)/2 si 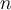n és imparell:
0%
❌
0%
0%
0%
View this question