Crowdly
Add to Chrome
MATH291 (DB425) Advanced Engineering Mathematics
Looking for MATH291 (DB425) Advanced Engineering Mathematics test answers and solutions? Browse our comprehensive collection of verified answers for MATH291 (DB425) Advanced Engineering Mathematics at moodle.uowplatform.edu.au.
Get instant access to accurate answers and detailed explanations for your course questions. Our community-driven platform helps students succeed!
Integrate the function f over the given region.f(x, y) = y2 ex4 over the triangular region in the first quadrant bounded by the lines x = y/6, x = 1, y = 0
0%
✅
0%
0%
View this question
Integrate the function f over the given region.f(x, y) =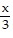 
+ 
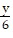over the trapezoidal region bounded by the x-axis, y-axis, line 
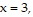and line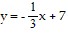 
100%
0%
0%
0%
View this question
Evaluate the integral.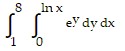
0%
0%
100%
0%
View this question
Evaluate the integral.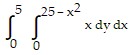
100%
0%
0%
0%
View this question
Find the volume under the surface z = f(x,y) and above the rectangle with the given boundaries.z = 6x2y; 0 ≤ x ≤ 4, 0 ≤ y ≤ 3
0%
0%
0%
✅
View this question
Integrate the function f over the given region.f(x, y) = e2x + 3y over the rectangle 0 ≤ x ≤ 1, 0 ≤ y ≤ 1
0%
0%
50%
0%
View this question
Evaluate the double integral over the given region.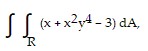
R: 0 ≤ x ≤ 1, 0 ≤ y ≤ 2
0%
0%
100%
0%
View this question
Evaluate the integral.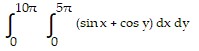
0%
✅
0%
0%
View this question
Solve the problem.Find the equation for the tangent plane to the surface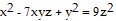 
at the point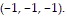 
0%
0%
0%
0%
View this question
Solve the problem.Find parametric equations for the normal line to the surface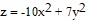 
at the point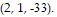 
0%
0%
0%
0%
View this question