Crowdly
Add to Chrome
MATH291 (DB425) Advanced Engineering Mathematics
Looking for MATH291 (DB425) Advanced Engineering Mathematics test answers and solutions? Browse our comprehensive collection of verified answers for MATH291 (DB425) Advanced Engineering Mathematics at moodle.uowplatform.edu.au.
Get instant access to accurate answers and detailed explanations for your course questions. Our community-driven platform helps students succeed!
Provide an appropriate response.Find the direction in which the function is increasing most rapidly at the point P0.f(x, y) = xey - ln(x), P0(3, 0)
50%
0%
0%
0%
View this question
Find the derivative of the function at P0 in the direction of u.f(x, y, z) = ln(x2 - 7y2 - 8z2), P0(-7, -7, -7), u = 3i + 4j
50%
0%
0%
0%
View this question
Find the derivative of the function at P0 in the direction of u.f(x, y) = ln(-7x + 9y), P0(10, -2), u = 6i + 8j
0%
0%
0%
0%
View this question
Compute the gradient of the function at the given point.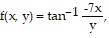
0%
0%
0%
0%
View this question
Use implicit differentiation to find the specified derivative at the given point.Find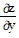 
at the point (6, 1, -1) for ln 
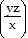- exy+z2 = 0.
0%
0%
100%
0%
View this question
Use implicit differentiation to find the specified derivative at the given point.Find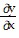 
at the point (1, 4, e6) for ln(xz)y + 2y3 = 0.
100%
0%
0%
0%
View this question
Use the chain rule to find the given partial derivative.Evaluate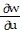 
at (u, v) = (1, 4) for the function w = xz + yz - z2; x = uv, y = uv, z = u.
0%
✅
0%
0%
View this question
Use the chain rule to find the given partial derivative.Evaluate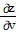 
at (u, v) = (5, 3) for the function z = xy2 - ln x; x = eu+v, y = uv.
0%
0%
✅
0%
View this question
Find the domain and range for the function f(x,y).f(x, y) =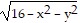 
✅
0%
0%
0%
View this question