Dirichlet test states that if a_n is a decreasing sequence with \lim_{n\to...
✅ The verified answer to this question is available below. Our community-reviewed solutions help you understand the material better.
Dirichlet test states that if 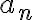 a_n is a decreasing sequence with
a_n is a decreasing sequence with 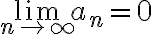 \lim_{n\to \infty}a_n=0, and
\lim_{n\to \infty}a_n=0, and 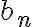 b_n is a sequence such that its partial sums
b_n is a sequence such that its partial sums 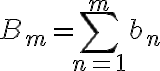 B_m=\sum_{n=1}^m b_n is bounded, then the series
B_m=\sum_{n=1}^m b_n is bounded, then the series 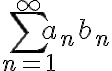 \sum_{n=1}^{\infty} a_nb_n is converging. We are going to test the convergence of
\sum_{n=1}^{\infty} a_nb_n is converging. We are going to test the convergence of 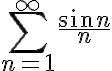 \sum_{n=1}^{\infty}\frac{\sin n}{n}. Which of the following claims are True regarding the correct choices and statements about
\sum_{n=1}^{\infty}\frac{\sin n}{n}. Which of the following claims are True regarding the correct choices and statements about 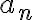 a_n and
a_n and 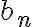 b_n for the Dirichlet Test?
b_n for the Dirichlet Test?
0%
0%
0%
0%
0%
0%
0%