When the Ratio Test fails, i.e. when \lim_{n\to\infty}\frac{u_n}{u_{n+1}}=1 , ...
✅ The verified answer to this question is available below. Our community-reviewed solutions help you understand the material better.
When the Ratio Test fails, i.e. when 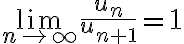 \lim_{n\to\infty}\frac{u_n}{u_{n+1}}=1, we can use the Raabe's Test. The test states that the associated series converges/diverges according to
\lim_{n\to\infty}\frac{u_n}{u_{n+1}}=1, we can use the Raabe's Test. The test states that the associated series converges/diverges according to 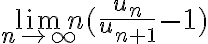 \lim_{n\to\infty}n(\frac{u_n}{u_{n+1}}-1) is greater/less than 1. Which of the following series fails the Ratio Test but passes the Raabe's Test for convergence/divergence?
\lim_{n\to\infty}n(\frac{u_n}{u_{n+1}}-1) is greater/less than 1. Which of the following series fails the Ratio Test but passes the Raabe's Test for convergence/divergence?
0%
0%
✅
✅
0%
✅