Crowdly

Add to Chrome

Universities
online.uom.lk
In24-S1-MA1014 - Mathematics

In24-S1-MA1014 - Mathematics

Looking for In24-S1-MA1014 - Mathematics test answers and solutions? Browse our comprehensive collection of verified answers for In24-S1-MA1014 - Mathematics at online.uom.lk.

Get instant access to accurate answers and detailed explanations for your course questions. Our community-driven platform helps students succeed!

Image failed to load

View this question

Image failed to load

View this question

Consider the function f(x)=-x^2 for $x \leq 1$ x \leq 1 and f(x)=x^3 for x>1. Which of the following are True?

$\lim_{x\to 1^-} f'(x)=-2$ \lim_{x\to 1^-} f'(x)=-2

$\lim_{x\to 1^+} f(x)=1$ \lim_{x\to 1^+} f(x)=1

f is right continuous at 1.

$\lim_{x\to 1^+} f'(x)=3$ \lim_{x\to 1^+} f'(x)=3

$\lim_{x\to 1^-} f(x)=(-1)^+$ \lim_{x\to 1^-} f(x)=(-1)^+

$\lim_{x\to 1^+} f(x)=1^+$ \lim_{x\to 1^+} f(x)=1^+

$\lim_{x\to 1^-} f'(x)=(-2)^-$ \lim_{x\to 1^-} f'(x)=(-2)^-

f is left continuous at 1.

$\lim_{x\to 1} f(x)$ \lim_{x\to 1} f(x) does not exist

f is right differentiable at 1 with $f'_{+}(1)=3$ f'_{+}(1)=3

f is left differentiable at 1 with $f'_{-}(1)=-2$ f'_{-}(1)=-2

f is differentiable at 1

f is continuous at 1.

View this question

View this question

View this question

Image failed to load

View this question

Image failed to load

Image failed to load

View this question

Let $f:[a,b]\rightarrow \mathbb{R}$ f:[a,b]\rightarrow \mathbb{R} be continuous and f(a) < 0 < f(b) . Define $A=\{x \in [a,b]|f(x) < 0 \}$ A=\{x \in [a,b]|f(x) < 0 \} and consider the proof of the Intermediate Value Theorem. Which of the following claims are True?

There exists $c \in (a,b)$ c \in (a,b) such that f(c) = 0 and $c= \sup A$ c= \sup A .

If $\sup A=c \in (a,b)$ \sup A=c \in (a,b) and f(c) > 0 then there are upper bounds of A to the left of c and that is a contradiction.

If $\sup A=c \in (a,b)$ \sup A=c \in (a,b) and f(c) > 0 then there are elements of A to the left of c and that is a contradiction.

If $\sup A=c \in (a,b)$ \sup A=c \in (a,b) and f(c) < 0 then there are elements of A to the right of c and that is a contradiction.

If $\sup A=a$ \sup A=a then there are elements of is A to the right of a and that is a contradiction.

f(a) < 0, therefore $a \in A$ a \in A and A is a non-empty subset of $\mathbb{R}$ \mathbb{R}.

If $\sup A=c \in (a,b)$ \sup A=c \in (a,b) and f(c) < 0 then there are upper bounds of A to the right of c and that is a contradiction.

If $\sup A=a$ \sup A=a then there are upper bounds of A to the right of a and that is a contradiction.

If A is a non-empty subset of $\mathbb{R}$ \mathbb{R} then it has a supremum, $\sup A\in \mathbb{R}$ \sup A\in \mathbb{R}.

If

Image failed to load: \sup A=b

\sup A=b then there are upper bounds of

A to the left of

b and that is a contradiction.

If

Image failed to load: \sup A=b

\sup A=b then there are elements of

A to the left of

b and that is a contradiction.

View this question

None of these.

View this question

When the Ratio Test fails, i.e. when 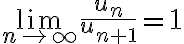$\lim_{n\to\infty}\frac{u_n}{u_{n+1}}=1$ \lim_{n\to\infty}\frac{u_n}{u_{n+1}}=1, we can use the Raabe's Test. The test states that the associated series converges/diverges according to 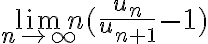$\lim_{n\to\infty}n(\frac{u_n}{u_{n+1}}-1)$ \lim_{n\to\infty}n(\frac{u_n}{u_{n+1}}-1) is greater/less than 1. Which of the following series fails the Ratio Test but passes the Raabe's Test for convergence/divergence?

$\sum_{n=1}^{\infty}\frac{1}{\sqrt{n}}$ \sum_{n=1}^{\infty}\frac{1}{\sqrt{n}}

$\sum_{n=1}^{\infty}\frac{1}{n}$ \sum_{n=1}^{\infty}\frac{1}{n}

$\sum_{n=1}^{\infty}\frac{1}{n^2(n+1)^2}$ \sum_{n=1}^{\infty}\frac{1}{n^2(n+1)^2}

$\sum_{n=1}^{\infty}\frac{1}{n^2}$ \sum_{n=1}^{\infty}\frac{1}{n^2}

$\sum_{n=1}^{\infty}\frac{1}{\sqrt{n}\sqrt{n+1}}$ \sum_{n=1}^{\infty}\frac{1}{\sqrt{n}\sqrt{n+1}}

$\sum_{n=1}^{\infty}\frac{1}{n(n+1)}$ \sum_{n=1}^{\infty}\frac{1}{n(n+1)}

View this question

Previous
1
3
4
5
8
Next

Want instant access to all verified answers on online.uom.lk?

Get Unlimited Answers To Exam Questions - Install Crowdly Extension Now!

Add to Chrome

Telegram Instagram TikTok Question Bank

Terms of Use Contact Us

Add to Chrome

Add to Chrome