Matematika
Looking for Matematika test answers and solutions? Browse our comprehensive collection of verified answers for Matematika at lms.smktarunabhakti.sch.id.
Get instant access to accurate answers and detailed explanations for your course questions. Our community-driven platform helps students succeed!
Turunan Hasil Bagi Fungsi Aljabar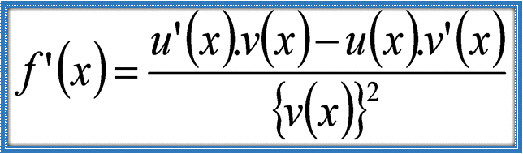 Turunan hasil bagi adalah metode dalam kalkulus untuk mencari turunan dari fungsi yang berbentuk pembagian antara dua fungsi lain. Ketika kita memiliki suatu fungsi yang merupakan hasil bagi antara fungsi pembilang dan fungsi penyebut, kita tidak bisa hanya menurunkan masing-masing secara terpisah dan membaginya begitu saja. Ada aturan khusus yang harus diikuti agar hasil turunan yang diperoleh benar dan akurat.Aturan turunan hasil bagi melibatkan proses menurunkan kedua fungsi, baik pembilang maupun penyebut, lalu mengkombinasikan hasil turunannya dengan cara tertentu yang memperhitungkan bagaimana perubahan pembilang dan penyebut mempengaruhi keseluruhan fungsi. Proses ini memastikan bahwa perubahan pada kedua fungsi tersebut dipertimbangkan dengan tepat sehingga hasil akhirnya mencerminkan laju perubahan fungsi hasil bagi tersebut secara menyeluruh.Penggunaan aturan ini sangat penting terutama saat fungsi yang kita hadapi tidak dapat disederhanakan lebih dulu atau berbentuk kompleks. Dengan mengikuti aturan ini, kita bisa menghitung turunan fungsi hasil bagi dengan tepat, yang selanjutnya membantu dalam berbagai aplikasi seperti menentukan kemiringan garis singgung, menemukan titik maksimum atau minimum suatu fungsi, serta dalam analisis dan pemodelan matematis yang melibatkan rasio dua fungsi.Selain menjadi alat yang kuat dalam kalkulus, pemahaman tentang turunan hasil bagi juga memperdalam wawasan kita tentang bagaimana dua fungsi saling berinteraksi melalui operasi pembagian dan bagaimana perubahan kecil pada fungsi-fungsi tersebut berdampak pada hasil bagi keseluruhan. Hal ini membuat konsep turunan hasil bagi tidak hanya berguna dalam matematika, tetapi juga dalam banyak disiplin ilmu lain yang membutuhkan analisis perubahan dan hubungan antar variabel.Cocokkan setiap pertanyaan di kolom A dengan jawaban yang sesuai di kolom B.
Turunan hasil bagi adalah metode dalam kalkulus untuk mencari turunan dari fungsi yang berbentuk pembagian antara dua fungsi lain. Ketika kita memiliki suatu fungsi yang merupakan hasil bagi antara fungsi pembilang dan fungsi penyebut, kita tidak bisa hanya menurunkan masing-masing secara terpisah dan membaginya begitu saja. Ada aturan khusus yang harus diikuti agar hasil turunan yang diperoleh benar dan akurat.Aturan turunan hasil bagi melibatkan proses menurunkan kedua fungsi, baik pembilang maupun penyebut, lalu mengkombinasikan hasil turunannya dengan cara tertentu yang memperhitungkan bagaimana perubahan pembilang dan penyebut mempengaruhi keseluruhan fungsi. Proses ini memastikan bahwa perubahan pada kedua fungsi tersebut dipertimbangkan dengan tepat sehingga hasil akhirnya mencerminkan laju perubahan fungsi hasil bagi tersebut secara menyeluruh.Penggunaan aturan ini sangat penting terutama saat fungsi yang kita hadapi tidak dapat disederhanakan lebih dulu atau berbentuk kompleks. Dengan mengikuti aturan ini, kita bisa menghitung turunan fungsi hasil bagi dengan tepat, yang selanjutnya membantu dalam berbagai aplikasi seperti menentukan kemiringan garis singgung, menemukan titik maksimum atau minimum suatu fungsi, serta dalam analisis dan pemodelan matematis yang melibatkan rasio dua fungsi.Selain menjadi alat yang kuat dalam kalkulus, pemahaman tentang turunan hasil bagi juga memperdalam wawasan kita tentang bagaimana dua fungsi saling berinteraksi melalui operasi pembagian dan bagaimana perubahan kecil pada fungsi-fungsi tersebut berdampak pada hasil bagi keseluruhan. Hal ini membuat konsep turunan hasil bagi tidak hanya berguna dalam matematika, tetapi juga dalam banyak disiplin ilmu lain yang membutuhkan analisis perubahan dan hubungan antar variabel.Cocokkan setiap pertanyaan di kolom A dengan jawaban yang sesuai di kolom B.
| Kolom ASoal | Kolom BJawaban |
| 1. | a. -36 |
| 2. | b. 9 |
| 3. | c. -2 |
| 4. | d. 1 |
| 5. | e. -17 |
View this question
Turunan Hasil Bagi Fungsi Aljabar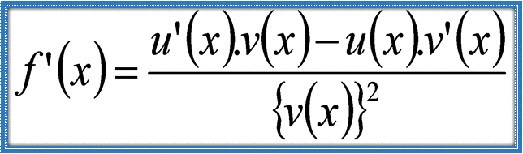 Turunan hasil bagi adalah metode dalam kalkulus untuk mencari turunan dari fungsi yang berbentuk pembagian antara dua fungsi lain. Ketika kita memiliki suatu fungsi yang merupakan hasil bagi antara fungsi pembilang dan fungsi penyebut, kita tidak bisa hanya menurunkan masing-masing secara terpisah dan membaginya begitu saja. Ada aturan khusus yang harus diikuti agar hasil turunan yang diperoleh benar dan akurat.Aturan turunan hasil bagi melibatkan proses menurunkan kedua fungsi, baik pembilang maupun penyebut, lalu mengkombinasikan hasil turunannya dengan cara tertentu yang memperhitungkan bagaimana perubahan pembilang dan penyebut mempengaruhi keseluruhan fungsi. Proses ini memastikan bahwa perubahan pada kedua fungsi tersebut dipertimbangkan dengan tepat sehingga hasil akhirnya mencerminkan laju perubahan fungsi hasil bagi tersebut secara menyeluruh.Penggunaan aturan ini sangat penting terutama saat fungsi yang kita hadapi tidak dapat disederhanakan lebih dulu atau berbentuk kompleks. Dengan mengikuti aturan ini, kita bisa menghitung turunan fungsi hasil bagi dengan tepat, yang selanjutnya membantu dalam berbagai aplikasi seperti menentukan kemiringan garis singgung, menemukan titik maksimum atau minimum suatu fungsi, serta dalam analisis dan pemodelan matematis yang melibatkan rasio dua fungsi.Selain menjadi alat yang kuat dalam kalkulus, pemahaman tentang turunan hasil bagi juga memperdalam wawasan kita tentang bagaimana dua fungsi saling berinteraksi melalui operasi pembagian dan bagaimana perubahan kecil pada fungsi-fungsi tersebut berdampak pada hasil bagi keseluruhan. Hal ini membuat konsep turunan hasil bagi tidak hanya berguna dalam matematika, tetapi juga dalam banyak disiplin ilmu lain yang membutuhkan analisis perubahan dan hubungan antar variabel.Cocokkan setiap pertanyaan di kolom A dengan jawaban yang sesuai di kolom B.
Turunan hasil bagi adalah metode dalam kalkulus untuk mencari turunan dari fungsi yang berbentuk pembagian antara dua fungsi lain. Ketika kita memiliki suatu fungsi yang merupakan hasil bagi antara fungsi pembilang dan fungsi penyebut, kita tidak bisa hanya menurunkan masing-masing secara terpisah dan membaginya begitu saja. Ada aturan khusus yang harus diikuti agar hasil turunan yang diperoleh benar dan akurat.Aturan turunan hasil bagi melibatkan proses menurunkan kedua fungsi, baik pembilang maupun penyebut, lalu mengkombinasikan hasil turunannya dengan cara tertentu yang memperhitungkan bagaimana perubahan pembilang dan penyebut mempengaruhi keseluruhan fungsi. Proses ini memastikan bahwa perubahan pada kedua fungsi tersebut dipertimbangkan dengan tepat sehingga hasil akhirnya mencerminkan laju perubahan fungsi hasil bagi tersebut secara menyeluruh.Penggunaan aturan ini sangat penting terutama saat fungsi yang kita hadapi tidak dapat disederhanakan lebih dulu atau berbentuk kompleks. Dengan mengikuti aturan ini, kita bisa menghitung turunan fungsi hasil bagi dengan tepat, yang selanjutnya membantu dalam berbagai aplikasi seperti menentukan kemiringan garis singgung, menemukan titik maksimum atau minimum suatu fungsi, serta dalam analisis dan pemodelan matematis yang melibatkan rasio dua fungsi.Selain menjadi alat yang kuat dalam kalkulus, pemahaman tentang turunan hasil bagi juga memperdalam wawasan kita tentang bagaimana dua fungsi saling berinteraksi melalui operasi pembagian dan bagaimana perubahan kecil pada fungsi-fungsi tersebut berdampak pada hasil bagi keseluruhan. Hal ini membuat konsep turunan hasil bagi tidak hanya berguna dalam matematika, tetapi juga dalam banyak disiplin ilmu lain yang membutuhkan analisis perubahan dan hubungan antar variabel.Cocokkan setiap pertanyaan di kolom A dengan jawaban yang sesuai di kolom B.
| Kolom ASoal | Kolom BJawaban |
| 1. | a. -55 |
| 2. | b. 33 |
| 3. | c. 53 |
| 4. | d. -19 |
| 5. | e. -30 |
View this question
Integral Tentu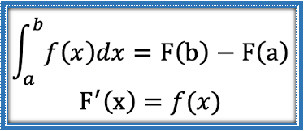 Integral tentu adalah proses menghitung luas daerah di bawah kurva fungsi pada interval tertentu. Berbeda dengan integral tak tentu yang menghasilkan fungsi umum dengan konstanta integrasi, integral tentu menghasilkan nilai angka yang mewakili luas tersebut. Interval yang digunakan ditentukan oleh batas bawah dan batas atas, biasanya ditulis dengan tanda integral yang diikuti oleh batas bawah di bawah simbol integral dan batas atas di atasnya.Proses menghitung integral tentu sering kali melibatkan menemukan fungsi primitif (antiturunan) dari fungsi yang diintegralkan, kemudian menghitung selisih nilai fungsi tersebut pada batas atas dan batas bawah. Metode ini dikenal sebagai Teorema Fundamental Kalkulus, yang menghubungkan operasi integral dan turunan secara langsung. Dengan menggunakan antiturunan, perhitungan integral menjadi lebih mudah dan praktis dibandingkan menghitung luas dengan cara penjumlahan kecil-kecil secara manual.Integral tentu banyak digunakan dalam berbagai bidang seperti fisika, teknik, ekonomi, dan statistika. Misalnya, untuk menghitung jarak yang ditempuh dari kecepatan yang berubah-ubah, atau menentukan total keuntungan berdasarkan fungsi pendapatan marginal. Selain itu, integral tentu juga digunakan untuk menghitung luas area, volume benda putar, dan berbagai aplikasi lain yang membutuhkan akumulasi nilai dalam interval tertentu.Pemahaman integral tentu sangat penting karena merupakan dasar bagi berbagai teknik lanjutan dalam kalkulus, seperti integral lipat, integral garis, dan aplikasi numerik. Menguasai konsep ini juga membantu dalam memahami bagaimana perubahan kecil diakumulasi menjadi perubahan besar dalam konteks matematika dan dunia nyata. Oleh karena itu, belajar integral tentu merupakan langkah penting dalam perjalanan mempelajari kalkulus secara menyeluruh.Hitung integral tentu:
Integral tentu adalah proses menghitung luas daerah di bawah kurva fungsi pada interval tertentu. Berbeda dengan integral tak tentu yang menghasilkan fungsi umum dengan konstanta integrasi, integral tentu menghasilkan nilai angka yang mewakili luas tersebut. Interval yang digunakan ditentukan oleh batas bawah dan batas atas, biasanya ditulis dengan tanda integral yang diikuti oleh batas bawah di bawah simbol integral dan batas atas di atasnya.Proses menghitung integral tentu sering kali melibatkan menemukan fungsi primitif (antiturunan) dari fungsi yang diintegralkan, kemudian menghitung selisih nilai fungsi tersebut pada batas atas dan batas bawah. Metode ini dikenal sebagai Teorema Fundamental Kalkulus, yang menghubungkan operasi integral dan turunan secara langsung. Dengan menggunakan antiturunan, perhitungan integral menjadi lebih mudah dan praktis dibandingkan menghitung luas dengan cara penjumlahan kecil-kecil secara manual.Integral tentu banyak digunakan dalam berbagai bidang seperti fisika, teknik, ekonomi, dan statistika. Misalnya, untuk menghitung jarak yang ditempuh dari kecepatan yang berubah-ubah, atau menentukan total keuntungan berdasarkan fungsi pendapatan marginal. Selain itu, integral tentu juga digunakan untuk menghitung luas area, volume benda putar, dan berbagai aplikasi lain yang membutuhkan akumulasi nilai dalam interval tertentu.Pemahaman integral tentu sangat penting karena merupakan dasar bagi berbagai teknik lanjutan dalam kalkulus, seperti integral lipat, integral garis, dan aplikasi numerik. Menguasai konsep ini juga membantu dalam memahami bagaimana perubahan kecil diakumulasi menjadi perubahan besar dalam konteks matematika dan dunia nyata. Oleh karena itu, belajar integral tentu merupakan langkah penting dalam perjalanan mempelajari kalkulus secara menyeluruh.Hitung integral tentu: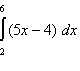
View this question
Integral Tak Tentu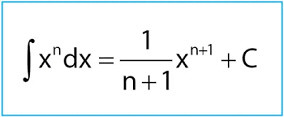 Integral tak tentu adalah salah satu konsep dasar dalam kalkulus integral yang digunakan untuk mencari fungsi asal dari suatu turunan. Dengan kata lain, integral tak tentu merupakan proses kebalikan dari turunan. Jika suatu fungsi diturunkan menghasilkan turunan tertentu, maka integral tak tentu dari turunan tersebut akan mengembalikan fungsi asalnya. Hasil dari integral tak tentu disebut sebagai fungsi antiturunan dan selalu disertai dengan konstanta integrasi, karena proses integrasi tidak bisa menentukan nilai konstanta tersebut secara pasti.Simbol yang digunakan untuk menyatakan integral tak tentu adalah tanda
Integral tak tentu adalah salah satu konsep dasar dalam kalkulus integral yang digunakan untuk mencari fungsi asal dari suatu turunan. Dengan kata lain, integral tak tentu merupakan proses kebalikan dari turunan. Jika suatu fungsi diturunkan menghasilkan turunan tertentu, maka integral tak tentu dari turunan tersebut akan mengembalikan fungsi asalnya. Hasil dari integral tak tentu disebut sebagai fungsi antiturunan dan selalu disertai dengan konstanta integrasi, karena proses integrasi tidak bisa menentukan nilai konstanta tersebut secara pasti.Simbol yang digunakan untuk menyatakan integral tak tentu adalah tanda 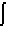 , diikuti oleh fungsi yang ingin diintegralkan, dan diakhiri dengan variabel yang digunakan. Proses ini disebut "mengintegralkan" fungsi. Sebagai contoh, jika suatu fungsi memiliki bentuk sederhana seperti f(x)=2x, maka hasil integral tak tentu dari fungsi ini adalah x
, diikuti oleh fungsi yang ingin diintegralkan, dan diakhiri dengan variabel yang digunakan. Proses ini disebut "mengintegralkan" fungsi. Sebagai contoh, jika suatu fungsi memiliki bentuk sederhana seperti f(x)=2x, maka hasil integral tak tentu dari fungsi ini adalah x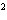 + C, di mana C adalah konstanta integrasi. Konstanta ini mencerminkan bahwa ada banyak fungsi yang memiliki turunan sama, hanya berbeda pada nilai tetapnya saja.Integral tak tentu sangat berguna dalam berbagai bidang matematika dan ilmu terapan, karena membantu dalam menemukan fungsi asli yang menggambarkan suatu fenomena berdasarkan laju perubahannya. Dalam fisika, misalnya, integral digunakan untuk menentukan posisi dari kecepatan, atau menentukan gaya dari percepatan. Demikian juga dalam ekonomi, integral membantu menentukan total pendapatan atau biaya dari fungsi marginal.Pemahaman tentang integral tak tentu merupakan fondasi penting sebelum mempelajari integral tentu dan aplikasi-aplikasinya. Untuk menguasainya, diperlukan pemahaman kuat terhadap aturan turunan, karena sebagian besar teknik integrasi merupakan kebalikan dari aturan-aturan turunan. Selain itu, keterampilan dalam aljabar dan pengenalan berbagai bentuk fungsi seperti polinomial, trigonometri, eksponensial, dan logaritma juga sangat membantu dalam proses integrasi.Cocokkan setiap pertanyaan di kolom A dengan jawaban yang sesuai di kolom B.
+ C, di mana C adalah konstanta integrasi. Konstanta ini mencerminkan bahwa ada banyak fungsi yang memiliki turunan sama, hanya berbeda pada nilai tetapnya saja.Integral tak tentu sangat berguna dalam berbagai bidang matematika dan ilmu terapan, karena membantu dalam menemukan fungsi asli yang menggambarkan suatu fenomena berdasarkan laju perubahannya. Dalam fisika, misalnya, integral digunakan untuk menentukan posisi dari kecepatan, atau menentukan gaya dari percepatan. Demikian juga dalam ekonomi, integral membantu menentukan total pendapatan atau biaya dari fungsi marginal.Pemahaman tentang integral tak tentu merupakan fondasi penting sebelum mempelajari integral tentu dan aplikasi-aplikasinya. Untuk menguasainya, diperlukan pemahaman kuat terhadap aturan turunan, karena sebagian besar teknik integrasi merupakan kebalikan dari aturan-aturan turunan. Selain itu, keterampilan dalam aljabar dan pengenalan berbagai bentuk fungsi seperti polinomial, trigonometri, eksponensial, dan logaritma juga sangat membantu dalam proses integrasi.Cocokkan setiap pertanyaan di kolom A dengan jawaban yang sesuai di kolom B.
| Kolom ASoal | Kolom BJawaban |
| 1. | a. |
| 2. | b. |
| 3. | c. |
| 4. | d. |
| 5. | e. |
View this question
Turunan Hasil Bagi Fungsi Aljabar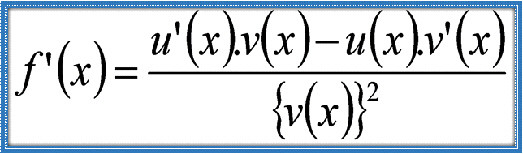 Turunan hasil bagi adalah metode dalam kalkulus untuk mencari turunan dari fungsi yang berbentuk pembagian antara dua fungsi lain. Ketika kita memiliki suatu fungsi yang merupakan hasil bagi antara fungsi pembilang dan fungsi penyebut, kita tidak bisa hanya menurunkan masing-masing secara terpisah dan membaginya begitu saja. Ada aturan khusus yang harus diikuti agar hasil turunan yang diperoleh benar dan akurat.Aturan turunan hasil bagi melibatkan proses menurunkan kedua fungsi, baik pembilang maupun penyebut, lalu mengkombinasikan hasil turunannya dengan cara tertentu yang memperhitungkan bagaimana perubahan pembilang dan penyebut mempengaruhi keseluruhan fungsi. Proses ini memastikan bahwa perubahan pada kedua fungsi tersebut dipertimbangkan dengan tepat sehingga hasil akhirnya mencerminkan laju perubahan fungsi hasil bagi tersebut secara menyeluruh.Penggunaan aturan ini sangat penting terutama saat fungsi yang kita hadapi tidak dapat disederhanakan lebih dulu atau berbentuk kompleks. Dengan mengikuti aturan ini, kita bisa menghitung turunan fungsi hasil bagi dengan tepat, yang selanjutnya membantu dalam berbagai aplikasi seperti menentukan kemiringan garis singgung, menemukan titik maksimum atau minimum suatu fungsi, serta dalam analisis dan pemodelan matematis yang melibatkan rasio dua fungsi.Selain menjadi alat yang kuat dalam kalkulus, pemahaman tentang turunan hasil bagi juga memperdalam wawasan kita tentang bagaimana dua fungsi saling berinteraksi melalui operasi pembagian dan bagaimana perubahan kecil pada fungsi-fungsi tersebut berdampak pada hasil bagi keseluruhan. Hal ini membuat konsep turunan hasil bagi tidak hanya berguna dalam matematika, tetapi juga dalam banyak disiplin ilmu lain yang membutuhkan analisis perubahan dan hubungan antar variabel.Cocokkan setiap pertanyaan di kolom A dengan jawaban yang sesuai di kolom B.
Turunan hasil bagi adalah metode dalam kalkulus untuk mencari turunan dari fungsi yang berbentuk pembagian antara dua fungsi lain. Ketika kita memiliki suatu fungsi yang merupakan hasil bagi antara fungsi pembilang dan fungsi penyebut, kita tidak bisa hanya menurunkan masing-masing secara terpisah dan membaginya begitu saja. Ada aturan khusus yang harus diikuti agar hasil turunan yang diperoleh benar dan akurat.Aturan turunan hasil bagi melibatkan proses menurunkan kedua fungsi, baik pembilang maupun penyebut, lalu mengkombinasikan hasil turunannya dengan cara tertentu yang memperhitungkan bagaimana perubahan pembilang dan penyebut mempengaruhi keseluruhan fungsi. Proses ini memastikan bahwa perubahan pada kedua fungsi tersebut dipertimbangkan dengan tepat sehingga hasil akhirnya mencerminkan laju perubahan fungsi hasil bagi tersebut secara menyeluruh.Penggunaan aturan ini sangat penting terutama saat fungsi yang kita hadapi tidak dapat disederhanakan lebih dulu atau berbentuk kompleks. Dengan mengikuti aturan ini, kita bisa menghitung turunan fungsi hasil bagi dengan tepat, yang selanjutnya membantu dalam berbagai aplikasi seperti menentukan kemiringan garis singgung, menemukan titik maksimum atau minimum suatu fungsi, serta dalam analisis dan pemodelan matematis yang melibatkan rasio dua fungsi.Selain menjadi alat yang kuat dalam kalkulus, pemahaman tentang turunan hasil bagi juga memperdalam wawasan kita tentang bagaimana dua fungsi saling berinteraksi melalui operasi pembagian dan bagaimana perubahan kecil pada fungsi-fungsi tersebut berdampak pada hasil bagi keseluruhan. Hal ini membuat konsep turunan hasil bagi tidak hanya berguna dalam matematika, tetapi juga dalam banyak disiplin ilmu lain yang membutuhkan analisis perubahan dan hubungan antar variabel.Cocokkan setiap pertanyaan di kolom A dengan jawaban yang sesuai di kolom B.
| Kolom ASoal | Kolom BJawaban |
| 1. | a. -22 |
| 2. | b. 48 |
| 3. | c. 17 |
| 4. | d. 37 |
| 5. | e. -27 |
View this question
Integral Tentu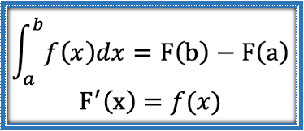 Integral tentu adalah proses menghitung luas daerah di bawah kurva fungsi pada interval tertentu. Berbeda dengan integral tak tentu yang menghasilkan fungsi umum dengan konstanta integrasi, integral tentu menghasilkan nilai angka yang mewakili luas tersebut. Interval yang digunakan ditentukan oleh batas bawah dan batas atas, biasanya ditulis dengan tanda integral yang diikuti oleh batas bawah di bawah simbol integral dan batas atas di atasnya.Proses menghitung integral tentu sering kali melibatkan menemukan fungsi primitif (antiturunan) dari fungsi yang diintegralkan, kemudian menghitung selisih nilai fungsi tersebut pada batas atas dan batas bawah. Metode ini dikenal sebagai Teorema Fundamental Kalkulus, yang menghubungkan operasi integral dan turunan secara langsung. Dengan menggunakan antiturunan, perhitungan integral menjadi lebih mudah dan praktis dibandingkan menghitung luas dengan cara penjumlahan kecil-kecil secara manual.Integral tentu banyak digunakan dalam berbagai bidang seperti fisika, teknik, ekonomi, dan statistika. Misalnya, untuk menghitung jarak yang ditempuh dari kecepatan yang berubah-ubah, atau menentukan total keuntungan berdasarkan fungsi pendapatan marginal. Selain itu, integral tentu juga digunakan untuk menghitung luas area, volume benda putar, dan berbagai aplikasi lain yang membutuhkan akumulasi nilai dalam interval tertentu.Pemahaman integral tentu sangat penting karena merupakan dasar bagi berbagai teknik lanjutan dalam kalkulus, seperti integral lipat, integral garis, dan aplikasi numerik. Menguasai konsep ini juga membantu dalam memahami bagaimana perubahan kecil diakumulasi menjadi perubahan besar dalam konteks matematika dan dunia nyata. Oleh karena itu, belajar integral tentu merupakan langkah penting dalam perjalanan mempelajari kalkulus secara menyeluruh.Hitung integral tentu:
Integral tentu adalah proses menghitung luas daerah di bawah kurva fungsi pada interval tertentu. Berbeda dengan integral tak tentu yang menghasilkan fungsi umum dengan konstanta integrasi, integral tentu menghasilkan nilai angka yang mewakili luas tersebut. Interval yang digunakan ditentukan oleh batas bawah dan batas atas, biasanya ditulis dengan tanda integral yang diikuti oleh batas bawah di bawah simbol integral dan batas atas di atasnya.Proses menghitung integral tentu sering kali melibatkan menemukan fungsi primitif (antiturunan) dari fungsi yang diintegralkan, kemudian menghitung selisih nilai fungsi tersebut pada batas atas dan batas bawah. Metode ini dikenal sebagai Teorema Fundamental Kalkulus, yang menghubungkan operasi integral dan turunan secara langsung. Dengan menggunakan antiturunan, perhitungan integral menjadi lebih mudah dan praktis dibandingkan menghitung luas dengan cara penjumlahan kecil-kecil secara manual.Integral tentu banyak digunakan dalam berbagai bidang seperti fisika, teknik, ekonomi, dan statistika. Misalnya, untuk menghitung jarak yang ditempuh dari kecepatan yang berubah-ubah, atau menentukan total keuntungan berdasarkan fungsi pendapatan marginal. Selain itu, integral tentu juga digunakan untuk menghitung luas area, volume benda putar, dan berbagai aplikasi lain yang membutuhkan akumulasi nilai dalam interval tertentu.Pemahaman integral tentu sangat penting karena merupakan dasar bagi berbagai teknik lanjutan dalam kalkulus, seperti integral lipat, integral garis, dan aplikasi numerik. Menguasai konsep ini juga membantu dalam memahami bagaimana perubahan kecil diakumulasi menjadi perubahan besar dalam konteks matematika dan dunia nyata. Oleh karena itu, belajar integral tentu merupakan langkah penting dalam perjalanan mempelajari kalkulus secara menyeluruh.Hitung integral tentu: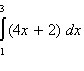
View this question
Integral Tak Tentu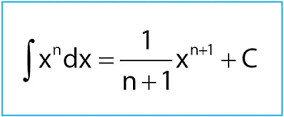 Integral tak tentu adalah salah satu konsep dasar dalam kalkulus integral yang digunakan untuk mencari fungsi asal dari suatu turunan. Dengan kata lain, integral tak tentu merupakan proses kebalikan dari turunan. Jika suatu fungsi diturunkan menghasilkan turunan tertentu, maka integral tak tentu dari turunan tersebut akan mengembalikan fungsi asalnya. Hasil dari integral tak tentu disebut sebagai fungsi antiturunan dan selalu disertai dengan konstanta integrasi, karena proses integrasi tidak bisa menentukan nilai konstanta tersebut secara pasti.Simbol yang digunakan untuk menyatakan integral tak tentu adalah tanda
Integral tak tentu adalah salah satu konsep dasar dalam kalkulus integral yang digunakan untuk mencari fungsi asal dari suatu turunan. Dengan kata lain, integral tak tentu merupakan proses kebalikan dari turunan. Jika suatu fungsi diturunkan menghasilkan turunan tertentu, maka integral tak tentu dari turunan tersebut akan mengembalikan fungsi asalnya. Hasil dari integral tak tentu disebut sebagai fungsi antiturunan dan selalu disertai dengan konstanta integrasi, karena proses integrasi tidak bisa menentukan nilai konstanta tersebut secara pasti.Simbol yang digunakan untuk menyatakan integral tak tentu adalah tanda 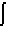 , diikuti oleh fungsi yang ingin diintegralkan, dan diakhiri dengan variabel yang digunakan. Proses ini disebut "mengintegralkan" fungsi. Sebagai contoh, jika suatu fungsi memiliki bentuk sederhana seperti f(x)=2x, maka hasil integral tak tentu dari fungsi ini adalah x
, diikuti oleh fungsi yang ingin diintegralkan, dan diakhiri dengan variabel yang digunakan. Proses ini disebut "mengintegralkan" fungsi. Sebagai contoh, jika suatu fungsi memiliki bentuk sederhana seperti f(x)=2x, maka hasil integral tak tentu dari fungsi ini adalah x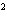 + C, di mana C adalah konstanta integrasi. Konstanta ini mencerminkan bahwa ada banyak fungsi yang memiliki turunan sama, hanya berbeda pada nilai tetapnya saja.Integral tak tentu sangat berguna dalam berbagai bidang matematika dan ilmu terapan, karena membantu dalam menemukan fungsi asli yang menggambarkan suatu fenomena berdasarkan laju perubahannya. Dalam fisika, misalnya, integral digunakan untuk menentukan posisi dari kecepatan, atau menentukan gaya dari percepatan. Demikian juga dalam ekonomi, integral membantu menentukan total pendapatan atau biaya dari fungsi marginal.Pemahaman tentang integral tak tentu merupakan fondasi penting sebelum mempelajari integral tentu dan aplikasi-aplikasinya. Untuk menguasainya, diperlukan pemahaman kuat terhadap aturan turunan, karena sebagian besar teknik integrasi merupakan kebalikan dari aturan-aturan turunan. Selain itu, keterampilan dalam aljabar dan pengenalan berbagai bentuk fungsi seperti polinomial, trigonometri, eksponensial, dan logaritma juga sangat membantu dalam proses integrasi.Cocokkan setiap pertanyaan di kolom A dengan jawaban yang sesuai di kolom B.
+ C, di mana C adalah konstanta integrasi. Konstanta ini mencerminkan bahwa ada banyak fungsi yang memiliki turunan sama, hanya berbeda pada nilai tetapnya saja.Integral tak tentu sangat berguna dalam berbagai bidang matematika dan ilmu terapan, karena membantu dalam menemukan fungsi asli yang menggambarkan suatu fenomena berdasarkan laju perubahannya. Dalam fisika, misalnya, integral digunakan untuk menentukan posisi dari kecepatan, atau menentukan gaya dari percepatan. Demikian juga dalam ekonomi, integral membantu menentukan total pendapatan atau biaya dari fungsi marginal.Pemahaman tentang integral tak tentu merupakan fondasi penting sebelum mempelajari integral tentu dan aplikasi-aplikasinya. Untuk menguasainya, diperlukan pemahaman kuat terhadap aturan turunan, karena sebagian besar teknik integrasi merupakan kebalikan dari aturan-aturan turunan. Selain itu, keterampilan dalam aljabar dan pengenalan berbagai bentuk fungsi seperti polinomial, trigonometri, eksponensial, dan logaritma juga sangat membantu dalam proses integrasi.Cocokkan setiap pertanyaan di kolom A dengan jawaban yang sesuai di kolom B.
| Kolom ASoal | Kolom BJawaban |
| 1. | a. |
| 2. | b. |
| 3. | c. 3x + c |
| 4. | d. |
| 5. | e. |
View this question
Integral Tentu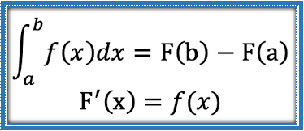 Integral tentu adalah proses menghitung luas daerah di bawah kurva fungsi pada interval tertentu. Berbeda dengan integral tak tentu yang menghasilkan fungsi umum dengan konstanta integrasi, integral tentu menghasilkan nilai angka yang mewakili luas tersebut. Interval yang digunakan ditentukan oleh batas bawah dan batas atas, biasanya ditulis dengan tanda integral yang diikuti oleh batas bawah di bawah simbol integral dan batas atas di atasnya.Proses menghitung integral tentu sering kali melibatkan menemukan fungsi primitif (antiturunan) dari fungsi yang diintegralkan, kemudian menghitung selisih nilai fungsi tersebut pada batas atas dan batas bawah. Metode ini dikenal sebagai Teorema Fundamental Kalkulus, yang menghubungkan operasi integral dan turunan secara langsung. Dengan menggunakan antiturunan, perhitungan integral menjadi lebih mudah dan praktis dibandingkan menghitung luas dengan cara penjumlahan kecil-kecil secara manual.Integral tentu banyak digunakan dalam berbagai bidang seperti fisika, teknik, ekonomi, dan statistika. Misalnya, untuk menghitung jarak yang ditempuh dari kecepatan yang berubah-ubah, atau menentukan total keuntungan berdasarkan fungsi pendapatan marginal. Selain itu, integral tentu juga digunakan untuk menghitung luas area, volume benda putar, dan berbagai aplikasi lain yang membutuhkan akumulasi nilai dalam interval tertentu.Pemahaman integral tentu sangat penting karena merupakan dasar bagi berbagai teknik lanjutan dalam kalkulus, seperti integral lipat, integral garis, dan aplikasi numerik. Menguasai konsep ini juga membantu dalam memahami bagaimana perubahan kecil diakumulasi menjadi perubahan besar dalam konteks matematika dan dunia nyata. Oleh karena itu, belajar integral tentu merupakan langkah penting dalam perjalanan mempelajari kalkulus secara menyeluruh.Hitung integral tentu:
Integral tentu adalah proses menghitung luas daerah di bawah kurva fungsi pada interval tertentu. Berbeda dengan integral tak tentu yang menghasilkan fungsi umum dengan konstanta integrasi, integral tentu menghasilkan nilai angka yang mewakili luas tersebut. Interval yang digunakan ditentukan oleh batas bawah dan batas atas, biasanya ditulis dengan tanda integral yang diikuti oleh batas bawah di bawah simbol integral dan batas atas di atasnya.Proses menghitung integral tentu sering kali melibatkan menemukan fungsi primitif (antiturunan) dari fungsi yang diintegralkan, kemudian menghitung selisih nilai fungsi tersebut pada batas atas dan batas bawah. Metode ini dikenal sebagai Teorema Fundamental Kalkulus, yang menghubungkan operasi integral dan turunan secara langsung. Dengan menggunakan antiturunan, perhitungan integral menjadi lebih mudah dan praktis dibandingkan menghitung luas dengan cara penjumlahan kecil-kecil secara manual.Integral tentu banyak digunakan dalam berbagai bidang seperti fisika, teknik, ekonomi, dan statistika. Misalnya, untuk menghitung jarak yang ditempuh dari kecepatan yang berubah-ubah, atau menentukan total keuntungan berdasarkan fungsi pendapatan marginal. Selain itu, integral tentu juga digunakan untuk menghitung luas area, volume benda putar, dan berbagai aplikasi lain yang membutuhkan akumulasi nilai dalam interval tertentu.Pemahaman integral tentu sangat penting karena merupakan dasar bagi berbagai teknik lanjutan dalam kalkulus, seperti integral lipat, integral garis, dan aplikasi numerik. Menguasai konsep ini juga membantu dalam memahami bagaimana perubahan kecil diakumulasi menjadi perubahan besar dalam konteks matematika dan dunia nyata. Oleh karena itu, belajar integral tentu merupakan langkah penting dalam perjalanan mempelajari kalkulus secara menyeluruh.Hitung integral tentu: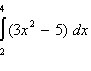
View this question
Turunan Hasil Bagi Fungsi Aljabar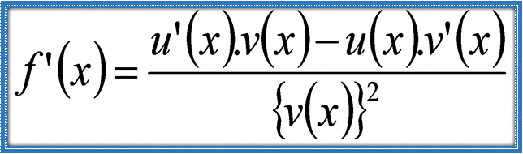 Turunan hasil bagi adalah metode dalam kalkulus untuk mencari turunan dari fungsi yang berbentuk pembagian antara dua fungsi lain. Ketika kita memiliki suatu fungsi yang merupakan hasil bagi antara fungsi pembilang dan fungsi penyebut, kita tidak bisa hanya menurunkan masing-masing secara terpisah dan membaginya begitu saja. Ada aturan khusus yang harus diikuti agar hasil turunan yang diperoleh benar dan akurat.Aturan turunan hasil bagi melibatkan proses menurunkan kedua fungsi, baik pembilang maupun penyebut, lalu mengkombinasikan hasil turunannya dengan cara tertentu yang memperhitungkan bagaimana perubahan pembilang dan penyebut mempengaruhi keseluruhan fungsi. Proses ini memastikan bahwa perubahan pada kedua fungsi tersebut dipertimbangkan dengan tepat sehingga hasil akhirnya mencerminkan laju perubahan fungsi hasil bagi tersebut secara menyeluruh.Penggunaan aturan ini sangat penting terutama saat fungsi yang kita hadapi tidak dapat disederhanakan lebih dulu atau berbentuk kompleks. Dengan mengikuti aturan ini, kita bisa menghitung turunan fungsi hasil bagi dengan tepat, yang selanjutnya membantu dalam berbagai aplikasi seperti menentukan kemiringan garis singgung, menemukan titik maksimum atau minimum suatu fungsi, serta dalam analisis dan pemodelan matematis yang melibatkan rasio dua fungsi.Selain menjadi alat yang kuat dalam kalkulus, pemahaman tentang turunan hasil bagi juga memperdalam wawasan kita tentang bagaimana dua fungsi saling berinteraksi melalui operasi pembagian dan bagaimana perubahan kecil pada fungsi-fungsi tersebut berdampak pada hasil bagi keseluruhan. Hal ini membuat konsep turunan hasil bagi tidak hanya berguna dalam matematika, tetapi juga dalam banyak disiplin ilmu lain yang membutuhkan analisis perubahan dan hubungan antar variabel.Cocokkan setiap pertanyaan di kolom A dengan jawaban yang sesuai di kolom B.
Turunan hasil bagi adalah metode dalam kalkulus untuk mencari turunan dari fungsi yang berbentuk pembagian antara dua fungsi lain. Ketika kita memiliki suatu fungsi yang merupakan hasil bagi antara fungsi pembilang dan fungsi penyebut, kita tidak bisa hanya menurunkan masing-masing secara terpisah dan membaginya begitu saja. Ada aturan khusus yang harus diikuti agar hasil turunan yang diperoleh benar dan akurat.Aturan turunan hasil bagi melibatkan proses menurunkan kedua fungsi, baik pembilang maupun penyebut, lalu mengkombinasikan hasil turunannya dengan cara tertentu yang memperhitungkan bagaimana perubahan pembilang dan penyebut mempengaruhi keseluruhan fungsi. Proses ini memastikan bahwa perubahan pada kedua fungsi tersebut dipertimbangkan dengan tepat sehingga hasil akhirnya mencerminkan laju perubahan fungsi hasil bagi tersebut secara menyeluruh.Penggunaan aturan ini sangat penting terutama saat fungsi yang kita hadapi tidak dapat disederhanakan lebih dulu atau berbentuk kompleks. Dengan mengikuti aturan ini, kita bisa menghitung turunan fungsi hasil bagi dengan tepat, yang selanjutnya membantu dalam berbagai aplikasi seperti menentukan kemiringan garis singgung, menemukan titik maksimum atau minimum suatu fungsi, serta dalam analisis dan pemodelan matematis yang melibatkan rasio dua fungsi.Selain menjadi alat yang kuat dalam kalkulus, pemahaman tentang turunan hasil bagi juga memperdalam wawasan kita tentang bagaimana dua fungsi saling berinteraksi melalui operasi pembagian dan bagaimana perubahan kecil pada fungsi-fungsi tersebut berdampak pada hasil bagi keseluruhan. Hal ini membuat konsep turunan hasil bagi tidak hanya berguna dalam matematika, tetapi juga dalam banyak disiplin ilmu lain yang membutuhkan analisis perubahan dan hubungan antar variabel.Cocokkan setiap pertanyaan di kolom A dengan jawaban yang sesuai di kolom B.
| Kolom ASoal | Kolom BJawaban |
| 1. | a. 31 |
| 2. | b. -23 |
| 3. | c. -19 |
| 4. | d. 21 |
| 5. | e. -1 |
View this question
Limit Fungsi Aljabar Limit adalah konsep dasar dalam matematika yang digunakan untuk memahami bagaimana sebuah fungsi mendekati nilai tertentu saat variabelnya mendekati suatu titik. Dalam dunia nyata, limit membantu kita melihat perilaku fungsi meskipun nilai pada titik tersebut mungkin tidak terdefinisi secara langsung. Misalnya, ketika kita ingin mengetahui nilai fungsi saat mendekati angka tertentu, limit menjadi alat yang sangat berguna.Pada dasarnya, limit membahas nilai yang "didekati" oleh fungsi f(x) ketika x mendekati suatu angka a. Misalnya, jika kita tulis lim
Limit adalah konsep dasar dalam matematika yang digunakan untuk memahami bagaimana sebuah fungsi mendekati nilai tertentu saat variabelnya mendekati suatu titik. Dalam dunia nyata, limit membantu kita melihat perilaku fungsi meskipun nilai pada titik tersebut mungkin tidak terdefinisi secara langsung. Misalnya, ketika kita ingin mengetahui nilai fungsi saat mendekati angka tertentu, limit menjadi alat yang sangat berguna.Pada dasarnya, limit membahas nilai yang "didekati" oleh fungsi f(x) ketika x mendekati suatu angka a. Misalnya, jika kita tulis lim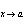 f(x)=L, artinya nilai fungsi f(x) mendekati L saat x mendekati a. Tidak selalu fungsi harus mencapai L pada x=a, tapi nilai fungsi tersebut harus semakin dekat dengan L ketika x semakin dekat dengan a.Penggunaan limit sangat penting dalam berbagai bidang teknik dan teknologi, terutama untuk memodelkan perubahan yang terjadi secara terus-menerus, seperti kecepatan, suhu, dan tekanan. Dengan memahami limit, kita bisa membuat prediksi dan analisis yang lebih tepat terhadap fenomena tersebut, yang tentu sangat membantu dalam bidang teknik dan produksi.Selain itu, limit menjadi dasar dari konsep turunan dan integral dalam kalkulus yang sering digunakan di bidang teknik. Pemahaman yang kuat tentang limit akan membantu siswa SMK dalam memahami materi yang lebih kompleks dan aplikasi praktis di dunia kerja nantinya. Oleh karena itu, memahami limit bukan hanya sekedar teori, tapi juga bekal penting dalam dunia teknik.Hasil dari :
f(x)=L, artinya nilai fungsi f(x) mendekati L saat x mendekati a. Tidak selalu fungsi harus mencapai L pada x=a, tapi nilai fungsi tersebut harus semakin dekat dengan L ketika x semakin dekat dengan a.Penggunaan limit sangat penting dalam berbagai bidang teknik dan teknologi, terutama untuk memodelkan perubahan yang terjadi secara terus-menerus, seperti kecepatan, suhu, dan tekanan. Dengan memahami limit, kita bisa membuat prediksi dan analisis yang lebih tepat terhadap fenomena tersebut, yang tentu sangat membantu dalam bidang teknik dan produksi.Selain itu, limit menjadi dasar dari konsep turunan dan integral dalam kalkulus yang sering digunakan di bidang teknik. Pemahaman yang kuat tentang limit akan membantu siswa SMK dalam memahami materi yang lebih kompleks dan aplikasi praktis di dunia kerja nantinya. Oleh karena itu, memahami limit bukan hanya sekedar teori, tapi juga bekal penting dalam dunia teknik.Hasil dari : 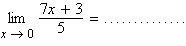
0%
0%
100%
0%
0%
View this question